What?
The Mondrian Puzzle is a puzzle that asks for a rectangle tiling of a integer-sided square. All used rectangles must be integer sided and pairwise non-congruential. The score of such a tiling (of which multiple are possible) is the difference between the areas of the largest and the smallest used rectangle. The ultimate challenge consists of finding a tiling that has the lowest score possible. Numberphile on YouTube explains the problem well.
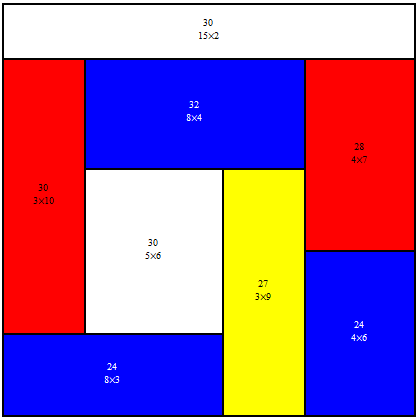
As an example, consider the image by Brady Haran above. It is a tiling of a 15 by 15 square. Each coloured rectangle contains its area and the dimension of the used rectangle. Note that it is a valid tiling as it covers the whole square and no congruential rectangles are used. The largest and smallest rectangle have an area of respectively 32 and 24, constituting a score of 8. Several people have come forward that they have found the lowest-score tilings for many sizes of squares. This optimality is proved by brute-force techniques by lack of a better method. A summary of presumably optimal solutions can be found on the OEIS website.
This website aims to collect not only proclaimed optimal solutions, but suboptimal ones as well. I hope it entices people to try and beat other people their scores.
Why?
Because it is fun! The Mondrian Puzzle is a problem that is easily explained but seems to be hard to solve (low-floor, high-ceiling). This is a property that many (commercially) succesful games such as Rush Hour, Reversi, Go, Chess, ... possess. Additionaly, researching seemingly inherently hard computational problems can lead to insights that aids other research. MathPickle presents the problem as a mathematical challenge for young pupils.How?
Check out the tilings on the View Tiling page to view all submissions so far. If you reckon that you can beat a score for some square size, grab a piece of paper or open up Excel and start tiling said square. You can also exert your programming skills to implement a brute force algorithm or maybe come up with some kind of heuristic technique*.
If you've found a better score than the one on the leaderboard, publish it on the Publish Tiling page.
* I'm very interested in determining the computational complexity of this problem and coming up with (meta)heuristic techniques. Feel free to contact me if you come up with something.